6 Simulaciones del proceso de Markov
Hemos realizado simulaciones utilizando el programa R, el cual nos permitirá visualizar el proceso de toma de decisiones en cada caso, i.e., si las personas siguieron o abandonaron las medidas de prevención. Además, mostraremos cómo son las recompensas asociadas a estas acciones.
Primero, definiremos la función que almacenará nuestro sistema de ecuaciones diferenciales.
EDO_SVVIR_Normalizado <- function(Time, State, Pars) {
with(as.list(c(State, Pars)), {
dS <- mu - (vbeta * S * I) - (mu + phi) * S + (omega * V_plus) + (xi * R)
dV_plus <- phi_plus * S - (mu + omega) * V_plus
dV_minus <- phi_minus * S - ((c * vbeta) * (V_minus * I)) - mu * V_minus
dI <- (vbeta * S * I) + ((c * vbeta) * (V_minus * I)) - (mu + vgamma) * I
dR <- (vgamma * I) - (mu + xi) * R
return(list(c(dS, dV_plus, dV_minus, dI, dR)))
})
}Ahora definiremos los valores de los parámetros necesarios para el sistema de ecuaciones diferenciales
# Limpiar la memoria de las variables
rm(list = ls())
# Paquetes necesarios para simulación
library(deSolve)
library(plotly)
# Sistema de ecuaciones
source("EDO_SVVIR_Normalizado.R", local = FALSE)
# Parámetros iniciales
mu <- 1 / (70 * 365)
omega <- 0.02
vgamma <- 1 / 14
p <- 0.7
vsigma <- 0.75
p_e <- p * vsigma
vT <- 35
phi_plus <- (-log(1 - p_e)) / vT
phi_minus <- (1 / vT) * log((1 - p_e) / (1 - p))
phi <- phi_plus + phi_minus
xi <- 1 / 30
vbeta <- 0.270En el siguiente código, mostraremos los pasos a seguir para realizar las simulaciones del proceso de Markov.
# Simulaciones del modelo
for (k in 1:n) {
t0 <- 0
T0 <- 65
t <- 1
RejillaTiempo <- seq(from = t0, to = T0, by = 1 / t)
vecTime <- numeric()
velec <- character()
vpsi <- numeric()
psi0 <- runif(1, 0.5, 2)
vpsi[1] <- psi0
c <- (1 - vsigma) * psi0
vpar <- c(
vbeta = vbeta, mu = mu, phi = phi, omega = omega,
xi = xi, phi_plus = phi_plus, phi_minus = phi_minus,
c = c, vgamma = vgamma
)
outSVVIR <- ode(yinicial, RejillaTiempo, EDO_SVVIR_Normalizado, vpar, method = "lsoda")
vPI <- numeric()
vPI[1] <- outSVVIR[T0, 5] * 10000
velec[1] <- if (0.5 < psi0 && psi0 < 0.9) {
"bien"
} else if (0.9 <= psi0 && psi0 <= 1.2) {
"normal"
} else {
"mal"
}
vecTime[1] <- T0
for (i in 1:3) {
T0 <- 65 + (100 * i)
RejillaTiempo <- seq(from = t0, to = T0, by = 1 / t)
vecTime[i + 1] <- T0
psi0 <- runif(1, 0.5, 2)
c <- (1 - vsigma) * psi0
vpsi[i + 1] <- psi0
vpar <- c(
vbeta = vbeta, mu = mu, phi = phi, omega = omega,
xi = xi, phi_plus = phi_plus, phi_minus = phi_minus,
c = c, vgamma = vgamma
)
outSVVIR <- ode(yinicial, RejillaTiempo, EDO_SVVIR_Normalizado, vpar, method = "lsoda")
vPI[i + 1] <- outSVVIR[T0, 5] * 10000
velec[i + 1] <- if (0.5 < psi0 && psi0 < 0.9) {
"bien"
} else if (0.9 <= psi0 && psi0 <= 1.2) {
"normal"
} else {
"mal"
}
}
MPI[, k] <- vPI
Mpsi[, k] <- vpsi
Mnames[, k] <- velec
}Siguiendo los códigos anteriores, podemos desarrollar las simulaciones necesarias para ilustrar la dinámica del proceso de Markov. En el siguiente escenario, se toma una decisión cada 100 días durante un año, y cada simulación representa un año diferente. En la siguiente gráfica, se muestran los diferentes valores de \(\psi\) asociados a las decisiones tomadas por las personas, ya sea seguir o no las medidas de prevención
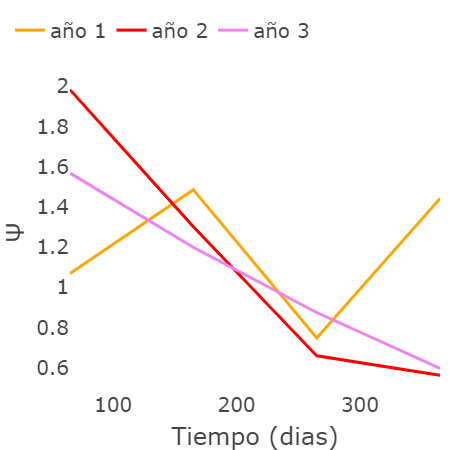
En la siguiente gráfica, mostramos cómo serían las recompensas correspondientes a cada una de las decisiones tomadas. Estas recompensas están relacionadas con la tabla presentada en la Sección 5 de este documento.
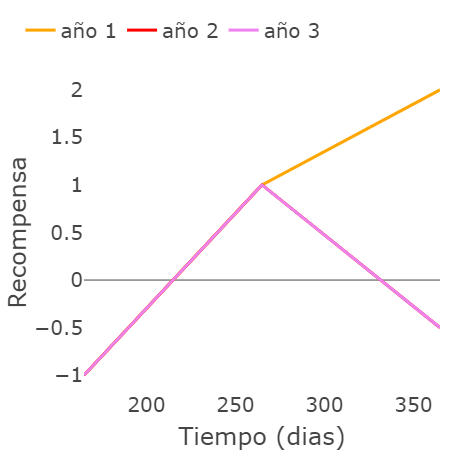
Finalmente, en esta última figura se muestran las consecuencias de tomar ese conjunto de decisiones en la prevalencia de la enfermedad.
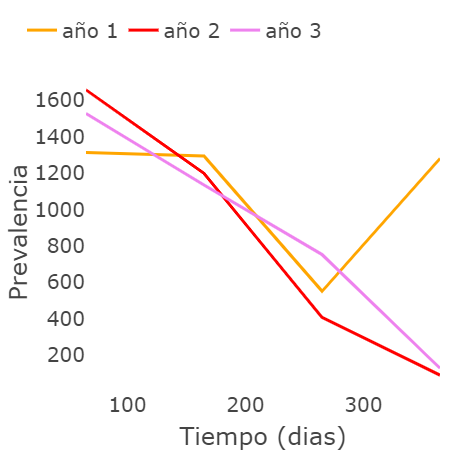
Con las figuras anteriores, se puede observar cómo los años 2 y 3 pueden tener la misma recompensa, aunque la selección de los valores de $\psi$ sea diferente. Finalmente, concluimos este proyecto con un video que explica en detalle los resultados mencionados.